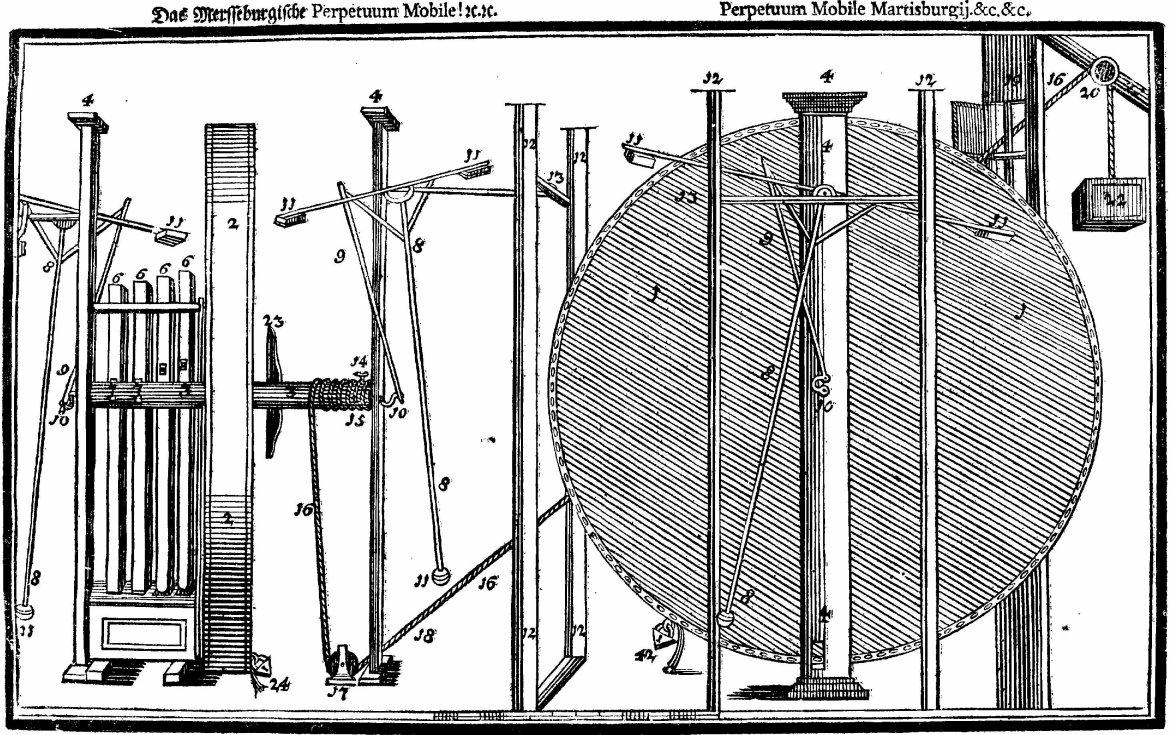
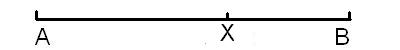|
Johann Bessler clearly knew much about the properties of the pentagon, pentagram and other geometrical shapes, as is evidenced by his use of the pentagram in most of his drawings and he admitted as much in his biographical details in ĎApologia Poeticaí. So it seemed to me that there might be more information to be extracted from his drawings than I had already found. One of the principle properties of the pentagram widely discussed and used in Besslerís time and before, is the presence of a concept known as the golden mean, golden ratio or golden section. Since long before the Renaissance, many artists and architects designed their works to accomodate the golden ratio in various forms - and the most popular has been the so-called golden rectangle, in which the ratio of the longer side to the shorter side observes the golden ratio. It was thought that this proportion was more pleasing to the eye, and mathematicians have studied the golden ratio because of its unique and interesting properties. In its simplest form, it is the division of a line in two sections, where the ratio between the smallest section and the largest section is identical to the ratio between the largest section and the entire length of the line. The ratio is about 1/1.618. A line, A to B, is divided at point X, so that the ratio of the two parts, the smaller XB to the larger AX is the same as the ratio of the larger part AX to the whole AB.
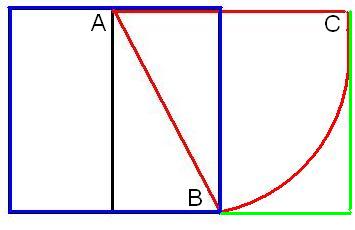
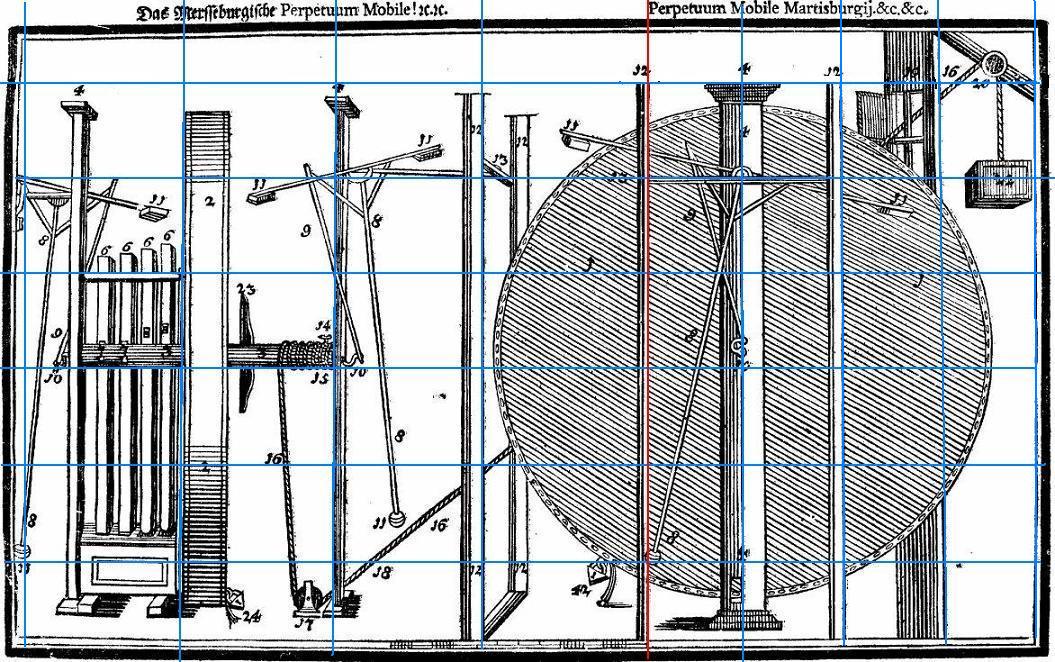
This same ratio can be applied to a rectangle and this is what Bessler did in his drawings. Draw a square (blue lines) and on the mid point on one side (A), place the sharp point of a pair of compasses. Extend the pencil point downwards to one of the opposite corners of the square (B), and then draw a curve (red) from B to C. The extended red line at the top of the square AC is in the golden ratio with the blue part of the same line.
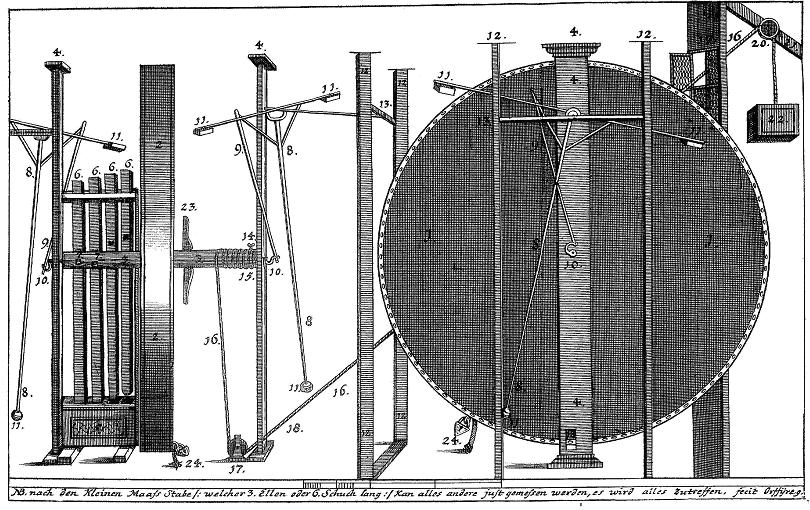
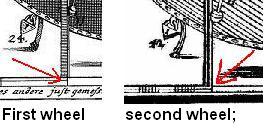
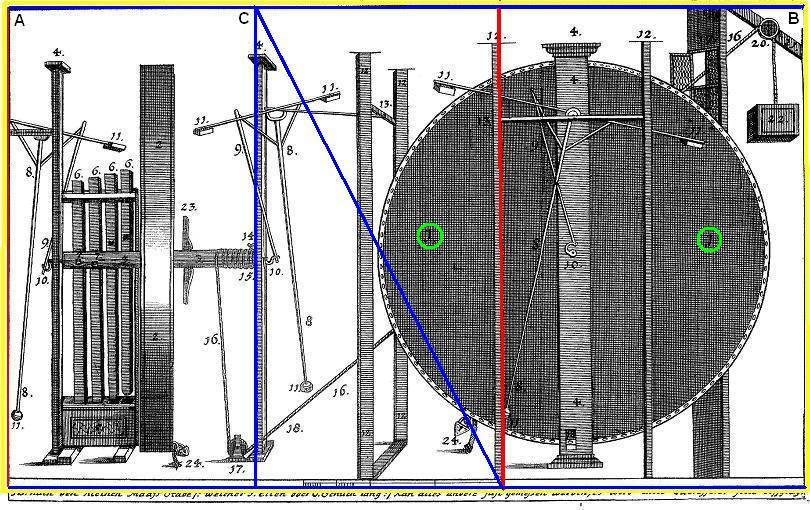
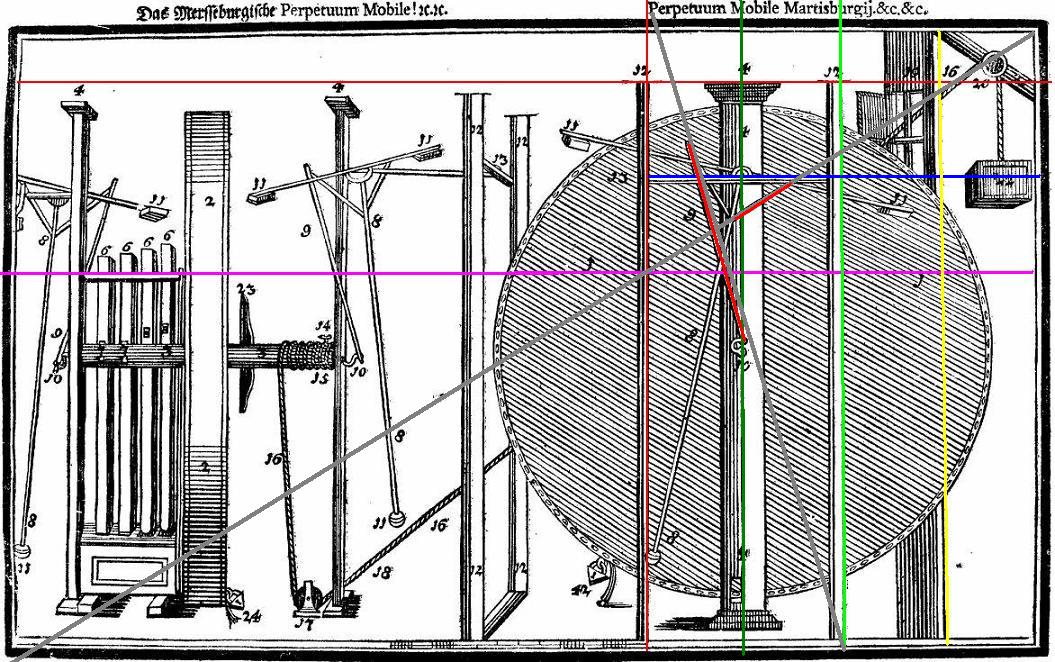
If you look at the enlargement below you will see that there is a small extension to the base of the left pillar supporting the pendulum. I have identified it with a red arrow. This does not seem very noticeable but it is when you relate it to the whole picture. The line in question forms the right side of a square of the left side of the whole picture, leaving to the right a rectangle.
The same applies to the second version of the wheel in Das Triumphirende. However there are differences. For instance in the first drawing the two number 1s (highlighted in green circles) are lower than they are in the second version. In the second drawing (below) they are shown placed slightly higher and now align (pink line) with the supporting strut at the top of the stamper unit. It may be that the first picture did not draw a clear enough connection with that line in which case it may assume importance later on in our research.
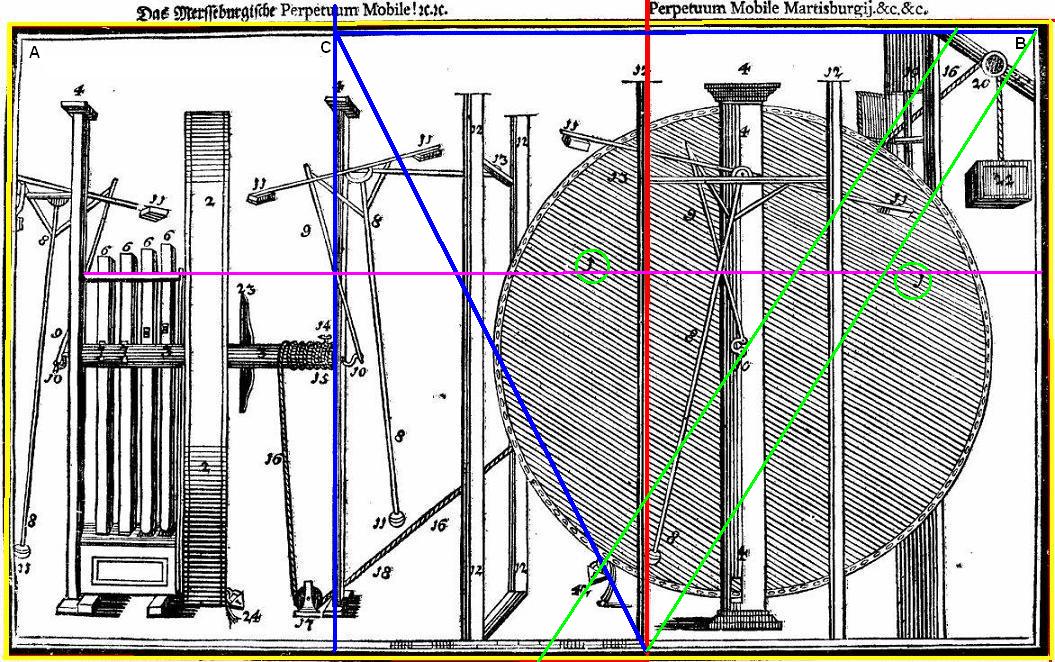
I got the same result with the first drawing, except that the upper point matched the lower side of the point where the pulley supporting beam is attached to the roof. To avoid a succession of bewildering lines, I shall in future drawings on this page, omit some of those already described. In the picture below, there appear to be two datum points, they have very clearly marked short horizontal lines on the top of the two pendulum-supprting pillars numbered 12. They are positioned on either side of the central pillar which supports the wheel. I have drawn a horizontal line (red) across them. The following lines all align with a feature in the drawing. From the way the enlarged piece is drawn I have assumed that it also refers to the right side of the picture - the rectangle. Notice that the rectangle is exactly bisected by the vertical green line which coincides with pillar (number 12) on the right side of the central pillar. Next I drew in the same pink line I referred to above which runs precisely between the two 1s. Notice that blue horizontal line also bisects the two squares occupying the upper part of the for-shortened rectangle. The yellow line bisects the right half of the rectangle and coincides with the right edge of the window wall. The dark green lines bisects the left half of the same rectangle, and is aligned on the centre of the main supporting pillar. There are two grey lines which run in perfect alignment with the two short arms supporting the pendulum, I have reddened them where they align. One grey line runs from the upper right of the complete drawing down to the left bottom. The other grey line runs from the top left of the rectangle to the bottom right of the same rectangle.
What does it all mean? I donít know. It clearly shows that Bessler was fully cognisant of the use in art of the golden mean and all its ramifications, but why was it included here? Is it another link to the pentagram and is that a reciprocal feature merely confirming each otherís existence ... only? Copyright © 2011 John Collins
|
| NavB[Home] [Bessler's name code] [Apologia Pentagram] [AP chronogram] [AP blanks & dashes] [AP Chapter 55] [Bessler's Initials] [Portrait pentagram] [More 1st portrait] [2nd portrait] [Pentagram in GB] [Golden Mean] [MT 55 pentagram] [MT Nos & letters] [MT 137 part one] [MT 137 part two] [MT 137 part three] [Bessler's Logo] [Drawing no codes] [5th DT Drawing] [Water wheel]wing |