|
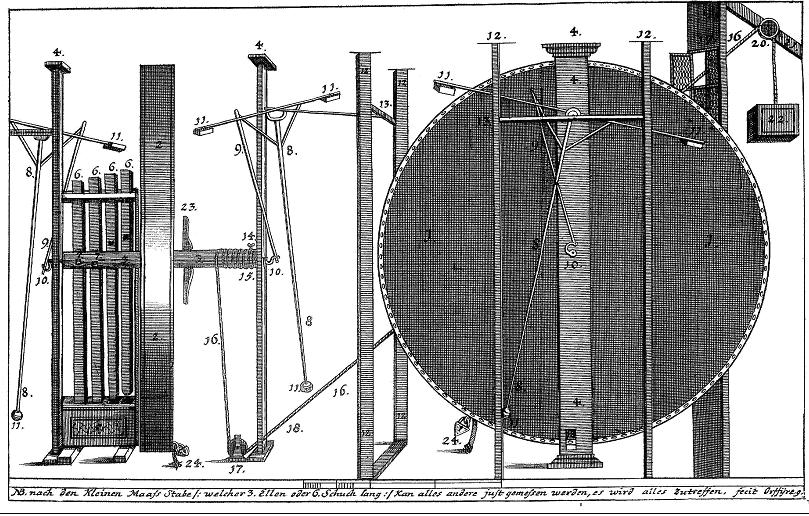
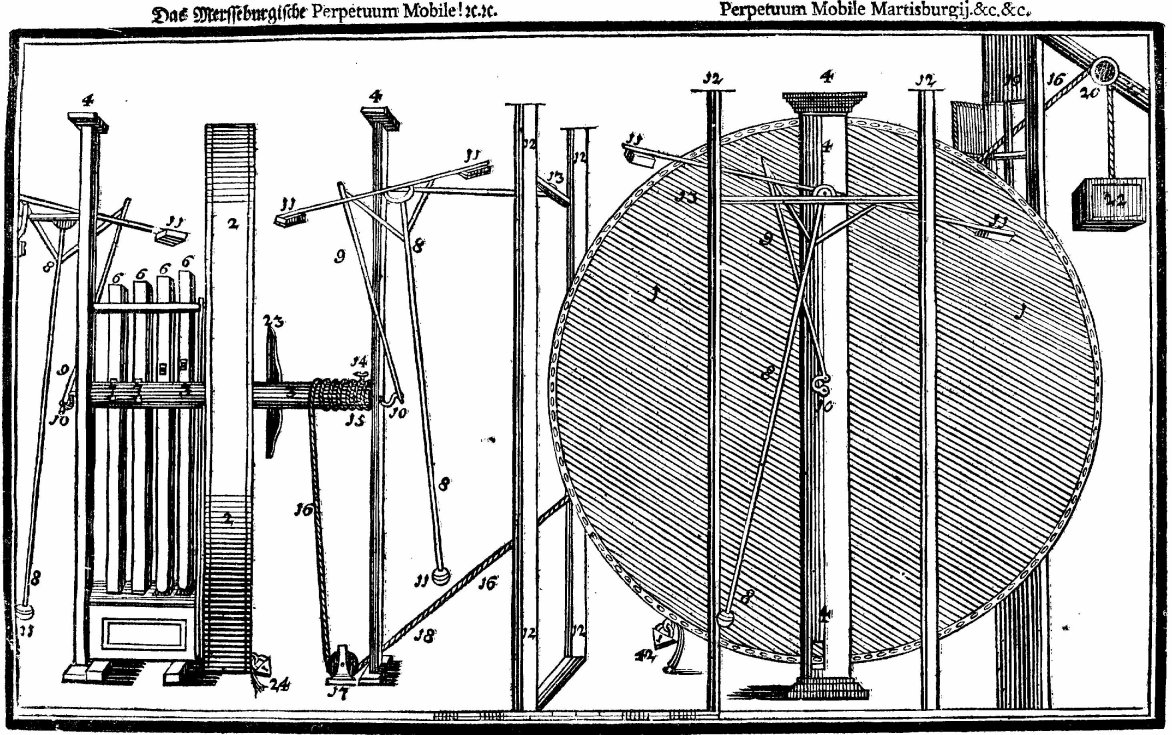
Johann Bessler produced four drawings ostensibly showing the external appearnce of his wheel, and two of them are so similar that one might wonder why he chose to redraw the second one. I have discussed the inclusion of a pentagram in both wheel drawings elsewhere but nothing has been said so far about the differences in the two drawings published by Bessler showing his wheel - and also the eccentric numbering of their parts. The first drawing comes from Bessler’s first publication, ‘Grundlicher Bericht’. The second one was printed in his most professional creation, ‘Das Triumphirende...’. and showed the external appearance of the same wheel with less detail. There appear on the face of it to be little difference other than the style of the drawing, and the differences shown are minimal - except for some typically Besseresque anomalies. For brevity and convenience I shall refer to the first drawing of the Merseberg wheel, as GB - and the second drawing as DT This drawing GB was the original one and has a heavier shading and it appears to be a better quality product than the later one.
The later one, DT below, looks clearer but is regarded as less well drawn.
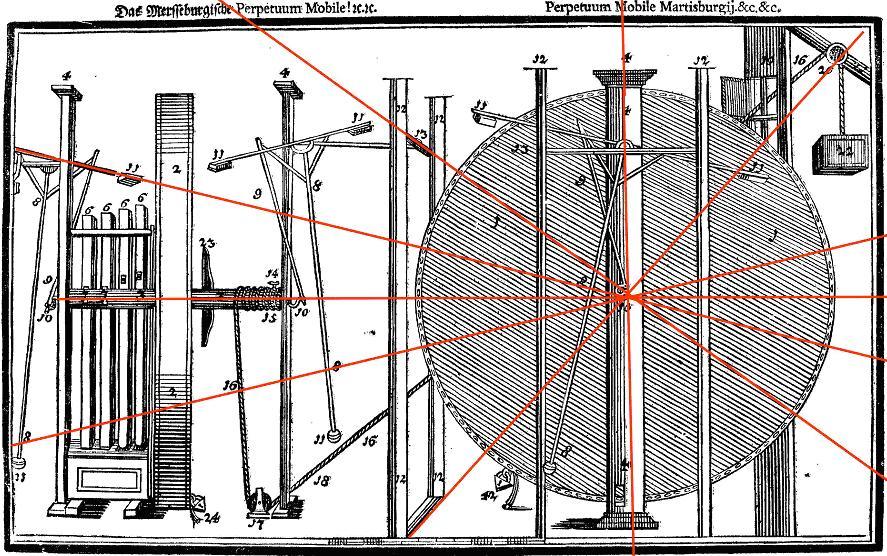
In GB the items are numbered from 1 to 24, in DT they are also numbered 1 to 24, plus the lone number 42. This looks like a simple printing error but of course I have always maintained that Bessler deliberately introduced such anomalies as clues. I’ll discuss this one later, first we need to look at some of the features apparent in the numbering. It becomes quite clear that some of the items are ‘over-numbered’. By that I mean that Bessler seems to have labelled the parts with a particular number more often than one might think was necessary. For example the main pillar supporting the wheel is numbered 4, four times. The slimmer pillars are numbered 12, and two of them to the left are numbered twice each, yet the other two are only numbered once each. Some numbers appear more often than others and not just because they are attached to more similar pieces. After number 18 the rest of the numbers are lone examples. I speculated that this was done to achieve a certain total, and having identified each part once with its number, he then sought to add to the total by labelling the same parts more than once. Obviously the higher numbers would make the jumps toward his desired total too big so he started at the lower end of the range and gradually added numbers until he had achieved his desired end. The numbers in GB total 649 and those in DT 633 - not apparently significant, but let’s look more closely. In GB there are two number 18’s yet one has been omitted in DT. In GB the number 5 is barely visible in the box at the bottom of the sideways-on wheel, yet it has clearly been omitted in DT. In GB the weights at the ends of the pendulums are numbered 11, there are eight of them, yet in DT one of them has been omitted. Finally in GB there are two number 24’s attached to the padlocks, yet in DT one of them has been reversed to become 42. Its almost impossible to see but in the first drawing, GB, the second number 18 is almost invisible, having been squeezed into the small hole through which the rope is supposed to pass. It is undoubtedly not there in DT. How can we explain all these anomalies? The omission of 5 and 18 in DT is explained by the fact that 5 is the most important number to Bessler because of its connection with the pentagram, and 18 degrees is the basic angle of the pentagram. Changing the number 24 to 42 can be explained by the omission of 18, because 42 - 24 = 18. He might have done this because of the difficulty of identifying both the the 5 and the second 18 in GB, and this lends credence to the idea that the numbers must add up to something significant. Bessler ensured we got this information by altering the second drawing. First he removed the 5 altogether plus he omitted one of the 11s, and 5 x 11=55. Then he assumed that we would compare the two drawings and realize that the second one not only omitted these two numbers, but also when totalled, the numbers add up to 633, and 633 from 649, the total of the numbers in GB, equalled 16 (or 5 + 11). So, in the first drawing (GB) the numbers, composed from 59 numbers, add up to 649, which is, interestingly, equal to 59 x 11 (both prime numbers). In the second drawing (DT) the numbers add up to 633, which is 16 short of the 649. In the second drawing the numbers 5 and one of the 11s has been omitted, which is why the second drawing does not match the 649 of the first drawing. In both drawings the picture cuts off the left hand end of the drawing and in the process cuts off one of the number 11 weights. If, in the first drawing, this is added to the 649 of the first drawing it produces the number 660, and because we then have 60 numbers, 660 divided by 60 equals 11, but more interestingly, 660 divided by 12 equals 55! How do we know that he intended us to figure this out? Because in both drawings there is an additional geometric feature which confirms it. I had noticed early on that the perspectives used in both drawings ran through the centre of the main wheel, and I just assumed that this was done from an artistic viewpoint. However I had already drawn all these lines in by extending them from one side to the other, in the process of which I noticed that there were twelve lines, marking out the face of a clock. I had wondered if this was deliberate but now I knew why it had been done. Twelve to six, three to nine, one to seven, eleven to five and ten to four all followed lines of perspective. To cinch the argument, the only one that did not, was two to eight o’clock, but interestingly the line exactly lined up the number eights attached to the weights, and there were two of them. That line defined the eight o’clock line. So extending all the perspective lines available to us, which cross in the centre of the wheel, provides us with a clock face. Using this we can divide up the picture and therefore the numbers by twelve. To recap, in the first drawing,649 = 59 x 11; add the missing 11, making 660 (60 x 11) the clock hints at 12, and 660/12=55! In the second drawing we can do the same - 633 + the missing 5 and the 11, plus the other 11 from the left side of the picture = 660. 660 divided by the twelve equals 55. Copyright © 2011 John Collins.
|
| NavB[Home] [Bessler's name code] [Apologia Pentagram] [AP chronogram] [AP blanks & dashes] [AP Chapter 55] [Bessler's Initials] [Portrait pentagram] [More 1st portrait] [2nd portrait] [Pentagram in GB] [Golden Mean] [MT 55 pentagram] [MT Nos & letters] [MT 137 part one] [MT 137 part two] [MT 137 part three] [Bessler's Logo] [Drawing no codes] [5th DT Drawing] [Water wheel]wing |